忙忙忙，盲盲盲，忙是为了自己的理想还是为了不让别人失望。

基本原理

Rabin加密算法简介:

Rabin算法是一种基于模平方和模平方根的非对称加密算法.

称a为x的算数平方, 称x为a的算数平方根

$$a=x^2⇔x=\sqrt[2]{x}$$

称a为x模m时的平方, 称x为a模m时的平方根

$$a≡x^2 mod m⇔x≡\sqrt[2]{x} mod m$$

称私钥p、q为两素数, 公钥 $n=p×q$. 对明文m和密文c, 定义以下加密过程(公钥加密过程):

$$c_i=m_i^2 mod n$$

对应的解密过程相当于求解以下的同余方程组：

$$m_i^2≡c_i mod n$$

根据中国剩余定理，同余方程有解当且仅当模互素，因此上述同余方程不可解(公钥无法解密公钥加密后的密文)。

但使用私钥p、q，可以通过以下方式得到明文：

令:

$$m_pi=\sqrt{c_i} mod p$$

$$m_qi=\sqrt{c_i} mod q$$

其中等式右边表示模平方根;

根据扩展欧几里德算法:

$$y_p∙p+y_q∙q=1$$

得到p、q的一个线性表示;

可以证明每一个密文对应四个原文，分别记为r、-r、s和-s，且有:

$$r=(y_p∙p∙m_q+y_q∙q∙m_p ) mod n$$

$$-r=n-r$$

$$s=(y_p∙p∙m_q-y_q∙q∙m_p ) mod n$$

$$-s=n-s$$

注意: 如果$p≡q≡3 (mod 4)$, 则

$$m_p=c^{1/4(p+1)} mod p$$

$$m_q=c^{1/4(q+1)} mod q$$

而一般情况下, $p≡q≡3 (mod 4)$是满足的.

当然，Rabin算法具有其致命的缺陷：一个密文对应四个明文。但此算法仍然包含了密码学中的基本概念和技巧，如单向函数、整数的因数分解等。

Rabin算法的安全性基于整数的因式分解问题：只有将公钥n正确分解为私钥p、q，才可以将公钥加密后的密文还原为原文，而通常p、q都会取相当大的素数，因此n也是一个非常大的数字；数字越大，其因式分解越困难。

漏洞场景分析

本案例中主要包括如下几个文件:

公钥: pubkey.pem

密文: flag.enc

同样的, 可以根据《小公钥指数攻击》中的 openssl 和 python 脚本进行提取其中的公钥内容和密文内容.这里指讲解通过python来解决问题, 通过openssl方法.

获取公钥内容

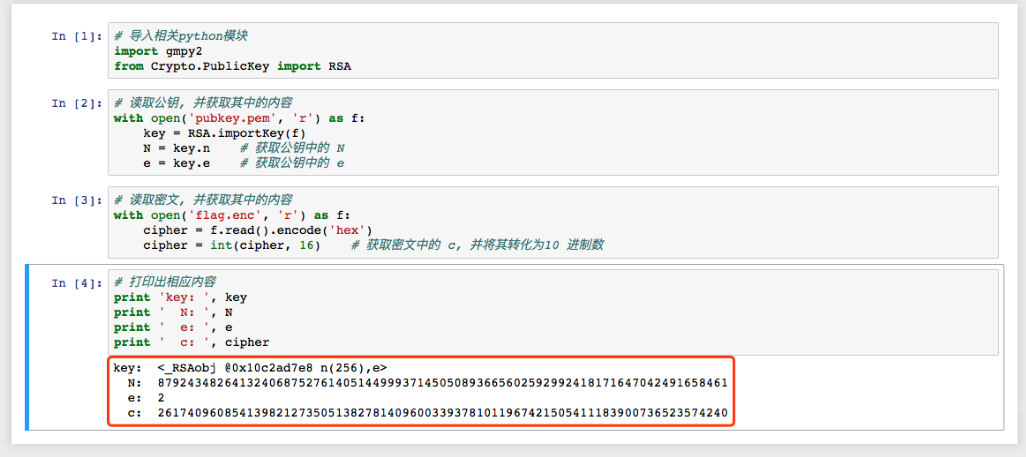
可以看到e = 2, 这里考虑到使用Rabin 算法, 首先分解一下 p 和 q , 得到如下

其中可以使用素数在线分解工具:

http://www.factordb.com

分解N

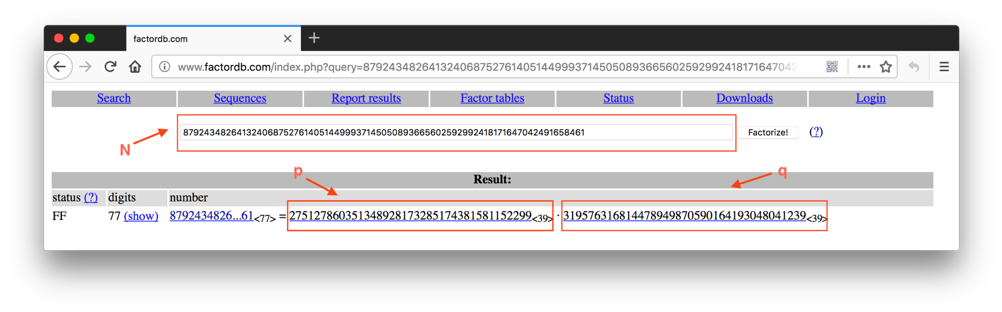
根据公式写相应的python脚本来得到明文

# -*-coding: utf-8 -*-  
import gmpy  

def n2s(num):  
    t = hex(num)[2:]  
    if len(t) % 2 == 1:  
        return ('0'+t).decode('hex')  
    return t.decode('hex')  

c = int(open('flag.enc','rb').read().encode('hex'),16)  # 密文 c  
p = 275127860351348928173285174381581152299             # 分解后的素数 p  
q = 319576316814478949870590164193048041239             # 分解后的素数 q  
n = p*q                                                 # 公钥 N  

# 根据中国剩余定理求解相应明文  
r = pow(c,(p+1)/4,p)  
s = pow(c,(q+1)/4,q)  
a = gmpy.invert(p,q)  
b = gmpy.invert(q,p)  
x =(a*p*s+b*q*r)%n  
y =(a*p*s-b*q*r)%n  

# 打印明文  
print n2s(x%n)  
print n2s((-x)%n)  
print n2s(y%n)  
print n2s((-y)%n)

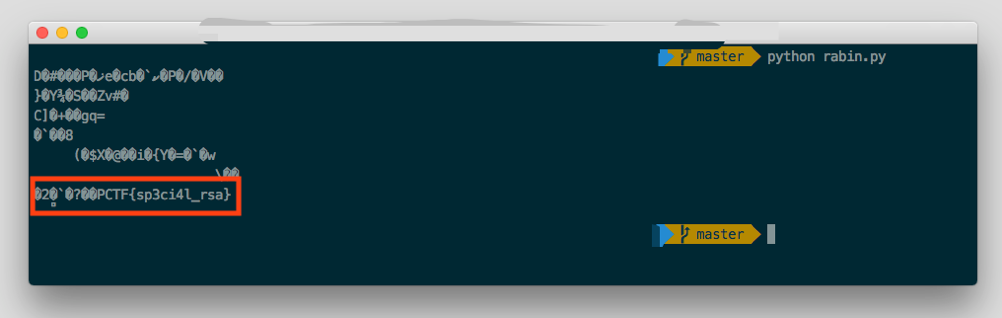
运行python脚本得到明文: