Coppersmith Method Attack

发表于 | 分类于

是空空荡荡、却嗡嗡作响。

基本原理

首先，我们来简单介绍一下 Coppersmith method 方法，该方法由 Don Coppersmith 提出，可以用来找到单变量或者二元变量的多项式在模某个整数下的根，这里我们主要以单变量为主，假设我们有如下的一个在模N意义下的多项式F:

$$F(x)=x^n+a_{n-1} x^{n-1}+ ···+ a_1 x+a_0$$

假设该多项式在模N意义下有一个根 \(x_0\), 这里我们令 \(x_0<M^{1/n}\) . 如果等号成立的话，显然只有 \(x^n\) 这一项，那0就是，也满足.

Coppersmith method 主要是通过Lenstra–Lenstra–Lovász lattice basis reduction algorithm (LLL) 方法来找到与该函数具有相同根 \(x0\) , 但有更小系数的多项式。

漏洞场景分析

Basic Broadcast Attack

攻击条件

如果一个用户使用同一个加密指数e加密了同一个密文，并发送给了其他e个用户。那么就会产生广播攻击。这一攻击由Håstad提出。

攻击原理

这里我们假设e为3，并且加密者使用了三个不同的模数 \(n_1\), \(n_2\), \(n_3\), 给三个不同的用户发送了加密后的消息m，如下:

$$c_1=m^3 mod n_1$$

$$c_2=m^3 mod n_2$$

$$c_3=m^3 mod n_3$$

这里我们假设 \(n_1\), \(n_2\), \(n_3\), 互相互素，不然，我们就可以直接进行分解，然后得到d，进而然后直接解密.

同时，我们假设 \(m<n_i,1≤i≤3\) , 如果这个条件不满足的话，就会使得情况变得比较复杂，这里我们暂不讨论.

既然他们互素，那么我们可以根据中国剩余定理，可得:

$$m^3≡C mod n_1 n_2 n_3$$

此外，既然 \(m<n_i,1≤i≤3\) , 那么我们知道:

$$m^3<n_1 n_2 n_3$$

并且:

$$C<m^3<n_1 n_2 n_3$$

那么:

$$m^3≡C$$

我们对C开三次根即可得到m的值。

对于较大的e来说，我们只是需要更多的明密文对。

漏洞利用

原文件是一个pcap包

pcap文件格式是常用的数据报存储格式，包括wireshark在内的主流抓包软件都可以生成这种格式的数据包.

从中提取数据

  1. 编写python脚本提取数据

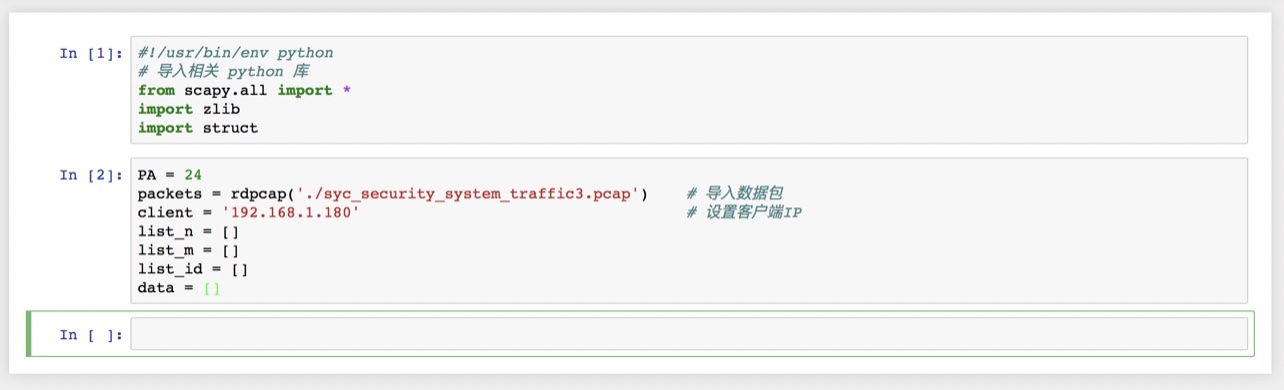
  1. 我们将文件内容打印出来, 可以看到其中包含有公钥 [N, e], 以及密文 c. 因此我们进行判断并提取出相关内容:

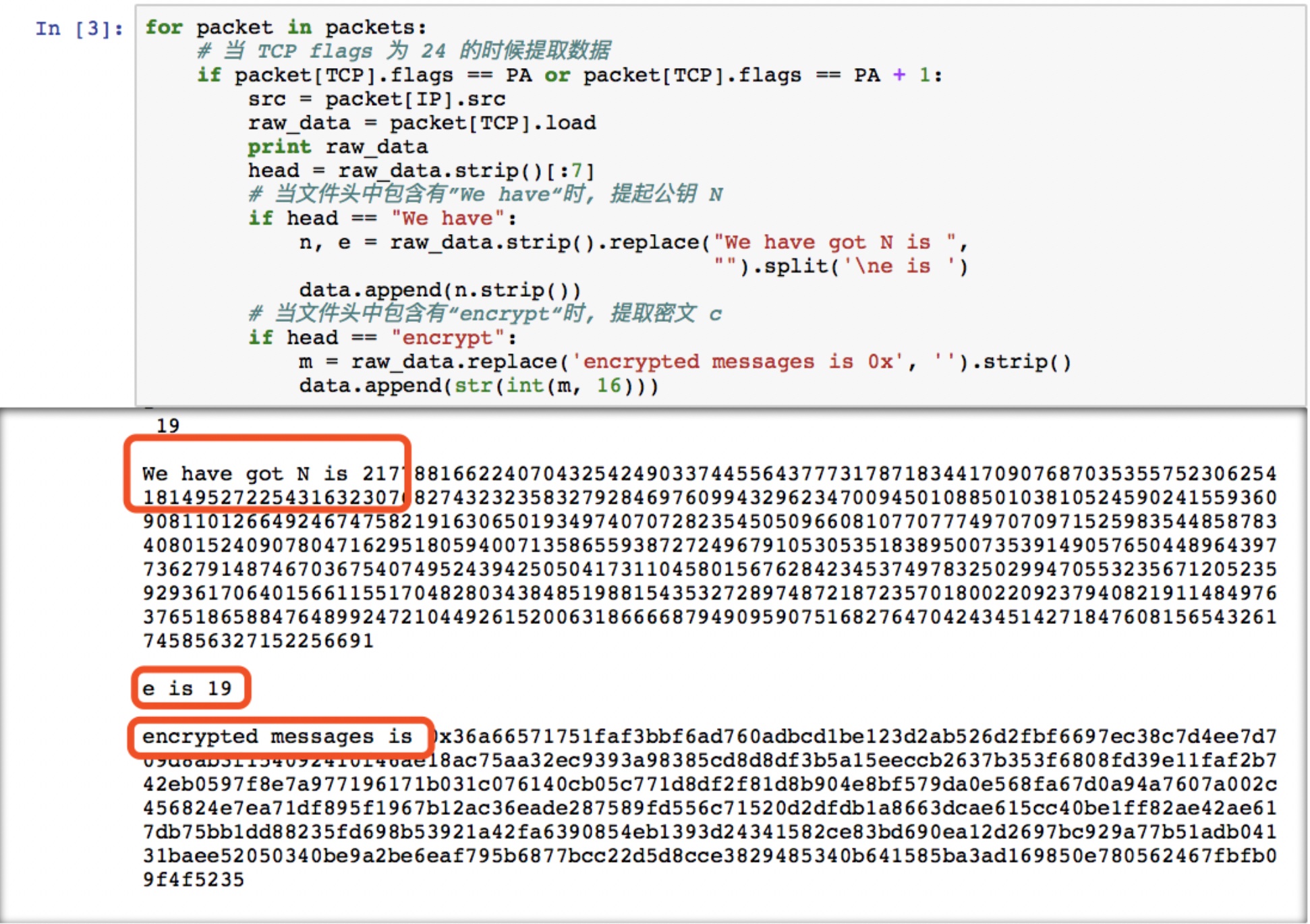
  1. 将数据保存到data.txt中, 方便进行下一步解密操作:

这时候就可以在当前文件夹中看到data.txt文件了:

数据看起来很麻烦, 接下来进行解密操作.

  1. 完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#!/usr/bin/env python  
  
from scapy.all import *  
import zlib  
import struct  
  
PA = 24  
packets = rdpcap('./syc_security_system_traffic3.pcap')  
client = '192.168.1.180'  
list_n = []  
list_m = []  
list_id = []  
data = []  
for packet in packets:  
    # TCP Flag PA 24 means carry data  
    if packet[TCP].flags == PA or packet[TCP].flags == PA + 1:  
        src = packet[IP].src  
        raw_data = packet[TCP].load  
        head = raw_data.strip()[:7]  
        if head == "We have":  
            n, e = raw_data.strip().replace("We have got N is ",  
                                            "").split('\ne is ')  
            data.append(n.strip())  
        if head == "encrypt":  
            m = raw_data.replace('encrypted messages is 0x', '').strip()  
            data.append(str(int(m, 16)))  
  
with open('./data.txt', 'w') as f: 
        for i in range(0, len(data), 2):  
        tmp = ','.join(s for s in data[i:i + 2])  
        f.write(tmp + '\n')

解密操作

  1. 导入相应python库并读取data.txt中到内容:

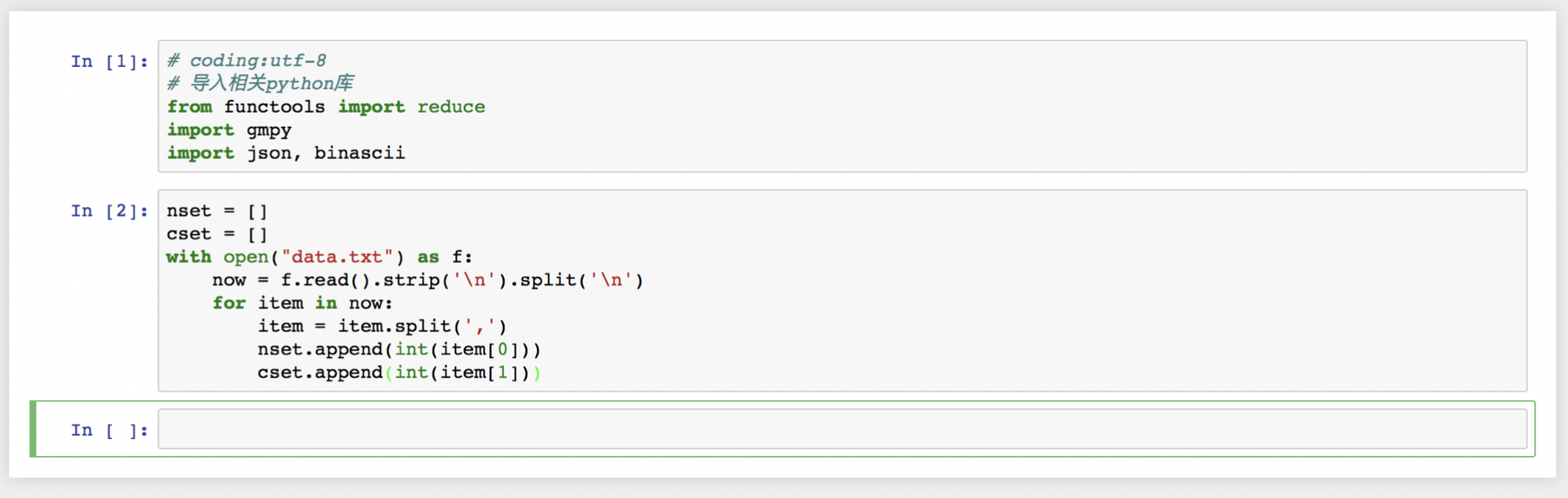
定义公钥N和密文c为数组, 将文件内容提取后写入数组中.

  1. 定义中国剩余定理, 前文已经介绍过. 在《Rabin加密》中有较为详细的介绍, 如仍有疑问, 可参见.

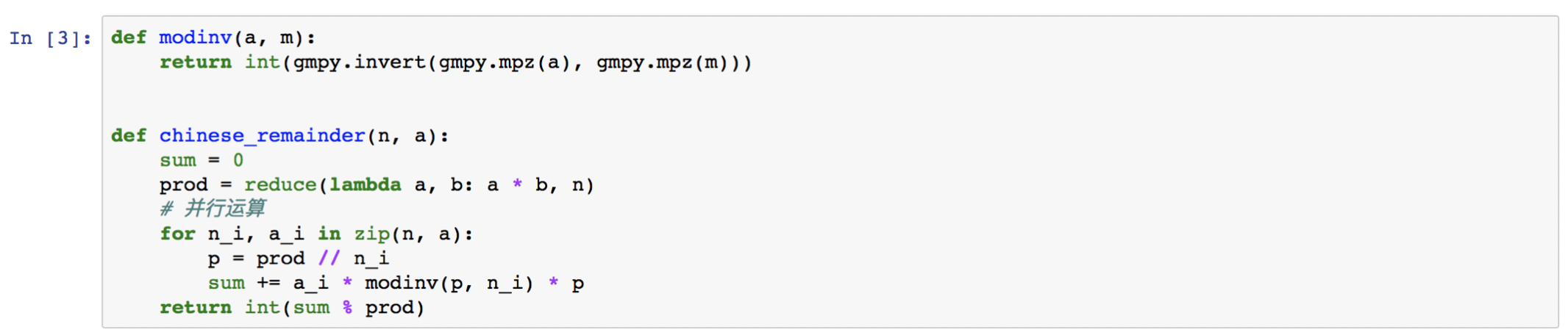
  1. 数据转换操作:

  1. 完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# coding:utf-8  
  
from functools import reduce  
import gmpy  
import json, binascii  
  
def modinv(a, m):  
    return int(gmpy.invert(gmpy.mpz(a), gmpy.mpz(m)))  
  
def chinese_remainder(n, a):  
    sum = 0  
    prod = reduce(lambda a, b: a * b, n)  
    # 并行运算  
    for n_i, a_i in zip(n, a):  
        p = prod // n_i  
        sum += a_i * modinv(p, n_i) * p  
    return int(sum % prod)  
  
nset = []  
cset = []  
with open("data.txt") as f:  
    now = f.read().strip('\n').split('\n')  
    for item in now:  
        item = item.split(',')  
        nset.append(int(item[0]))  
        cset.append(int(item[1]))  
  
m = chinese_remainder(nset, cset)  
m = int(gmpy.mpz(m).root(19)[0])  
print binascii.unhexlify(hex(m)[2:-1])